LAUSR

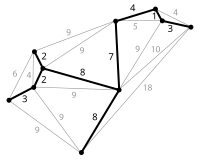
In this paper, we develop an efficient diagonal quadratic optimization formulation for minimum weight design problem subject to multiple constraints. A high‐efficiency computational approach of topology optimization is implemented within the framework of approximate reanalysis. The key point of the formulation is the introduction of the reciprocal‐type variables. The topology optimization seeking for minimum weight can be transformed as a sequence of quadratic program with separable and strictly positive definite Hessian matrix, thus can be solved by a sequential quadratic programming approach. A modified sensitivity filtering scheme is suggested to remove undesirable checkerboard patterns and mesh dependence. Several typical examples are provided to validate the presented approach. It is observed that the optimized structure can achieve lighter weight than those from the established method by the demonstrative numerical test. Considerable computational savings can be achieved without loss of accuracy of the final design for 3D structure. Moreover, the effects of multiple constraints and upper bound of the allowable compliance upon the optimized designs are investigated by numerical examples.