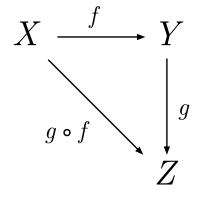
Photo from wikipedia
A shallow semantical embedding of free logic in classical higher-order logic is presented, which enables the off-the-shelf application of higher-order interactive and automated theorem provers for the formalisation and verification… Click to show full abstract
A shallow semantical embedding of free logic in classical higher-order logic is presented, which enables the off-the-shelf application of higher-order interactive and automated theorem provers for the formalisation and verification of free logic theories. Subsequently, this approach is applied to a selected domain of mathematics: starting from a generalization of the standard axioms for a monoid we present a stepwise development of various, mutually equivalent foundational axiom systems for category theory. As a side-effect of this work some (minor) issues in a prominent category theory textbook have been revealed. The purpose of this article is not to claim any novel results in category theory, but to demonstrate an elegant way to “implement” and utilize interactive and automated reasoning in free logic, and to present illustrative experiments.
Journal Title: Journal of Automated Reasoning
Year Published: 2019
Link to full text (if available)
Share on Social Media: Sign Up to like & get
recommendations!