LAUSR

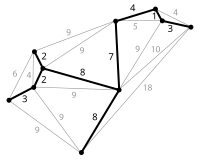
For an edge-weighted graph $$G=(V,E,w)$$G=(V,E,w), in which the vertices are partitioned into k clusters $$\mathcal {R}=\{R_1,R_2,\ldots ,R_k\}$$R={R1,R2,…,Rk}, a spanning tree T of G is a clustered spanning tree if T can be cut into k subtrees by removing $$k-1$$k-1 edges such that each subtree is a spanning tree for one cluster. In this paper, we show the inapproximability of finding a clustered spanning tree with minimum routing cost, where the routing cost is the total distance summed over all pairs of vertices. We present a 2-approximation for the case that the input is a complete weighted graph whose edge weights obey the triangle inequality. We also study a variant in which the objective function is the total distance summed over all pairs of vertices of different clusters. We show that the problem is polynomial-time solvable when the number of clusters k is 2 and NP-hard for $$k=3$$k=3. Finally, we propose a polynomial-time 2-approximation algorithm for the case of three clusters.