LAUSR

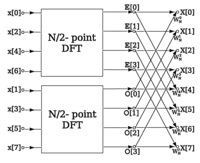
The quantum Fourier transform (QFT) is perhaps the furthermost central building block in creation quantum algorithms. In this work, we present a new approach to compute the standard quantum Fourier transform of the length $$ N = 2^{r} , \;r > 1 $$N=2r,r>1, which also is called the r-qubit discrete Fourier transform. The presented algorithm is based on the paired transform developed by authors. It is shown that the signal-flow graphs of the paired algorithms could be used for calculating the quantum Fourier and Hadamard transform with the minimum number of stages. The calculation of all components of the transforms is performed by the Hadamard gates and matrices of rotations and all simple NOT gates. The new presentation allows for implementing the QFT (a) by using only the r Hadamard gates and (b) organizing parallel computation in r stages. Also, the circuits for the length-2r fast Hadamard transform are described. Several mathematical illustrative examples of the order the $$ N = 4,\;8 $$N=4,8, and 16 cases are illustrated. Finally, the QFT for inputs being two, three and four qubits is described in detail.