LAUSR

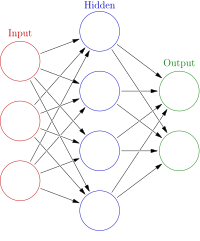
Abstract This paper deals with the development of an Artificial Neural Network methodology for the prediction of the liquid phase diffusion coefficient between species at infinite dilution in binary mixtures. The proposed methodology was implemented to estimate the diffusion coefficients with improved accuracy with respect to empirical correlations, which are widely used despite their significant errors, especially on organic mixtures. The final aim of the work is to propose a novel methodology to apply in industrial fields where the mass transport by diffusion between organic liquids plays a key role, e.g. the lubricant degradation and scraping due to the dilution with the liquid fuel in the engine combustion chamber and the dilution of heavy oils and bitumens with organic solvents. In spite of the classical use of Artificial Neural Networks, this work is based on the mutual support between a reference empirical correlation and the Neural Network model, where the former is used to directly calculate the diffusion coefficient while the latter is trained to correct the correlation's result depending on the bonds strength in the solvent and the solute. Moreover, since the prediction of the diffusion coefficient for new mixtures (i.e. where no experimental measures are available) with Artificial Neural Network models should not be taken blindly, a Bayesian Neural Network is implemented, since it is capable to provide the degree of uncertainty of its prediction. This Bayesian Neural Network, given a selection of fluid properties as input features, was trained on 263 experimental data collected from literature findings. The proposed methodology achieved the prediction of the 80% of the available data with absolute relative errors lower than 10%, while the most recognized empirical correlations predicted the same data with absolute relative errors from 30 to 45%. A proof of the reliability of this methodology is the fact that the experimental data corresponding to the points predicted with the higher errors however fall in the predicted uncertainty, whose average width is below the ±20% of the predicted mean.