LAUSR

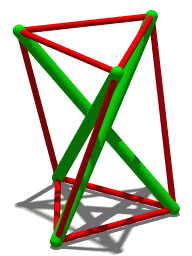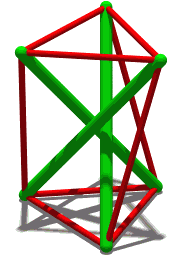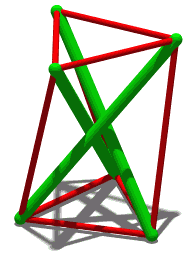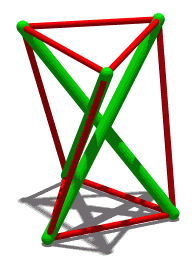
Abstract A group-theoretical method is proposed for form-finding of symmetric cable-strut structures. Only the given topology and structural symmetry are necessary for implementing this form-finding process. Irreducible representations for rigid-body translations along d directions are used to get the corresponding symmetry subspaces, which transform the original force density matrix into d small-sized block matrices. Therefore, significant simplification on the form-finding process is achieved. Numerical decomposition of these blocks is performed to find analytical sets of force densities and nodal coordinates, which satisfy the minimum required rank deficiencies of the blocks and indicate meaningful null spaces. On condition that the tangent stiffness matrix of the obtained configuration is positive definite, a non-degenerate d-dimensional stable cable-strut structure is built. Some examples specified by Cnv or Dn symmetry are presented. It shows that the proposed method is effective for searching feasible configurations of cable-strut structures with specific symmetries.