LAUSR

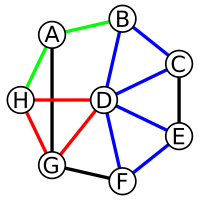
Abstract Given any real α ∈ [ 0 , 1 ] , the α-index of a graph G is the largest eigenvalue λ α ( G ) of the matrix A α ( G ) = α D ( G ) + ( 1 − α ) A ( G ) , where A ( G ) and D ( G ) stand for the adjacency matrix and the diagonal matrix of vertex degrees in G, respectively. In this paper, we determine the unique graph with maximum α-index among all graphs of order n with no 4-cycle and 5-cycle, respectively. These results partially answer a proposed problem in Nikiforov (2017) [7, Problem 24] .