LAUSR

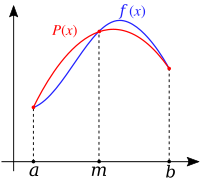
Abstract In this paper we established a numerical method for Equal Width (EW) Equation using Polynomial Scaling Functions. The EW equation is a simpler alternative to well known Korteweg de Vries (KdV) and regularized long wave (RLW) equations which have many applications in nonlinear wave phenomena. According to Polynomial scaling method, algebraic polynomials are used to get the orthogonality between the wavelets and corresponding scaling functions with respect to the Chebyshev weight. First we introduce polynomial scaling functions, how are the functions are approximated according to these and Operational matrix of derivatives are given. For time discretization of the function we use finite difference method with Rubin Graves linearization and polynomial scaling functions are used for the space discretization. The method is applied to four different problem and the obtained results are compared with the results in the literature and with the exact results to give the efficiency of the method.