LAUSR

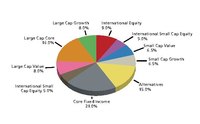
Decentralized investment management can be defined as the practice of having multiple managers implement investment strategies across different asset categories. It has been common practice due the presence of alternative investments or other asset classes which require high levels of specialization. However, it suffers from limited control of total fund characteristics such as total return, risk and liquidity. We model the investment process as an optimization problem in which we seek to maximize the flexibility for individual managers, while satisfying a set of desired long-term total portfolio characteristics of the fund. This process will allow firms to enable decentralized investment decisions without sacrificing the performance at the total fund level. The proposed optimization problem has a potentially large number of constraints, limiting the number of strategies below a practical level. We suggest a procedure to reduce the number of constraints before calling the optimization and include numerical results that support the effectiveness of the procedure. Also, investigated in this paper is the robust version of the proposed optimization.