LAUSR

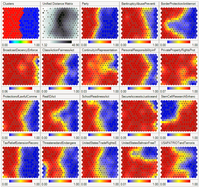
Extremely large-scale networks have received increasing attention in recent years. The development of big data and network science provides an unprecedented opportunity for research on these networks. However, it is difficult to perform analysis directly on numerous real networks due to their large size. A solution is to sample a subnetwork instead for detailed research. Unfortunately, the properties of the subnetworks could be substantially different from those of the original networks. In this context, a comprehensive understanding of the sampling methods would be crucial for network-based big data analysis. In our work, we find that the sampling deviation is the collective effect of both the network heterogeneity and the biases caused by the sampling methods themselves. Here, we study the widely used random node sampling (RNS), breadth-first search, and a hybrid method that falls between these two. We empirically and analytically investigate the differences in topological properties between the sampled network and the original network under these sampling methods. Empirically, the hybrid method has the advantage of preserving structural properties in most cases, which suggests that this method performs better with no additional information needed. However, not all the biases caused by sampling methods follow the same pattern. For instance, properties, such as link density, are better preserved by RNS. Finally, models are constructed to explain the biases concerning the size of giant connected components and link density analytically.