LAUSR

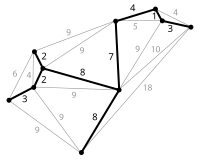
For a multi-agent system (MAS) with a directed weighted chain graph, this article studies the effect of adding reverse edges on its convergence rate. The introduction of weights leads to our research being more complex and challenging. Firstly, for the case of one reverse edge, there are two completely opposite conclusions about the effect of adding one reverse edge on the convergence rate under certain conditions, which is dependent on whether the end node of the reverse edge is the root node of the chain graph or not. Subsequently, we discuss the relative positions of two reverse edges in three cases and obtain the convergence rate of the whole network is determined by the ranges, the relative positions of these two reverse edges, and the sizes and distribution of weights in the directed weighted graph. Moreover, as the number of reverse edges increases, we overcome the complex relationships among multiple reverse edges and establish similar theories. Finally, some numerical examples are given to illustrate our main theorems. Our results generalise the results from unweighted directed graph to a weighted directed graph.