LAUSR

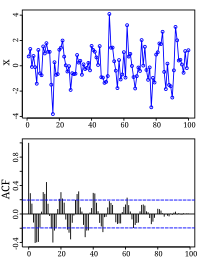
ABSTRACT This study considers the problem of testing for a parameter change in integer-valued time series models in which the conditional density of current observations is assumed to follow a Poisson distribution. As a test, we consider the CUSUM of the squares test based on the residuals from INGARCH models and find that the test converges weakly to the supremum of a Brownian bridge. A simulation study demonstrates its superiority to the residual and standardized residual-based CUSUM tests of Kang and Lee [Parameter change test for Poisson autoregressive models. Scand J Statist. 2014;41:1136–1152] and Lee and Lee [CUSUM tests for general nonlinear inter-valued GARCH models: comparison study. Ann Inst Stat Math. 2019;71:1033–1057.] as well as the CUSUM of squares test based on standardized residuals.