LAUSR

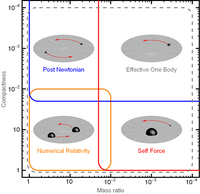
The effective one-body formalism of the gravitational two-body problem in general relativity is reconsidered in the light of recent scattering amplitude calculations. Based on the kinematic relationship between momenta and the effective potential, we consider an energy-dependent effective metric describing the scattering in terms of an effective one-body problem for the reduced mass. The identification of the effective metric simplifies considerably in isotropic coordinates when combined with a redefined angular momentum map. While the effective energy-dependent metric as expected is not unique, solutions can be chosen perturbatively in the post-Minkowskian expansion without the need to introduce nonmetric corrections. By a canonical transformation, our condition maps to the one based on the standard angular momentum map. Expanding our metric around the Schwarzschild solution we recover the solution based on additional nonmetric contributions.