LAUSR

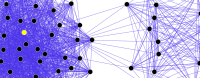
This paper is concerned with the robustness of the sustained oscillations predicted by an epidemic ODE model defined on contact networks. The model incorporates the spread of awareness among individuals and, moreover, a small inflow of imported cases. These cases prevent stochastic extinctions when we simulate the epidemics and, hence, they allow to check whether the average dynamics for the fraction of infected individuals are accurately predicted by the ODE model. Stochastic simulations confirm the existence of sustained oscillations for different types of random networks, with a sharp transition from a nonoscillatory asymptotic regime to a periodic one as the alerting rate of susceptible individuals increases from very small values. This abrupt transition to periodic epidemics of high amplitude is quite accurately predicted by the Hopf-bifurcation curve computed from the ODE model using the alerting rate and the infection transmission rate for aware individuals as tuning parameters.