LAUSR

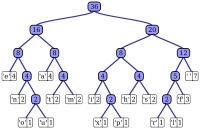
In the presented paper, we investigate the problem of finding the maximum possible cardinality of a dictionary of a prefix code for a string of a given length. Namely, we present a sharp proof of the cardinality of such a dictionary using results from the number theory. What is more, the presented formula is for the general case of a string over any, not just binary, alphabet. Furthermore, we give conditions on the existence of the so-called canonical dictionary for such a string, where the codewords of the dictionary have at most two different lengths, differing by one. Our approach is based on reformulating the problem of finding the maximum possible cardinality of a dictionary for a string of a given length as the problem of finding the maximum possible number of summands in the Kraft-Szillard partition of the number representing the length of the string, by solving a Diophantine equation related to the canonical partition of the number. One of the areas of applications of presented results is the security-estimate of ciphers based on prefix codes.