LAUSR

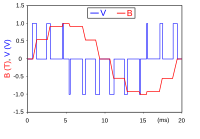
This study deals with a control problem for continuous-time linear time-invariant systems driven by a pulse-modulation-type control input. Although pulse-driven systems are nonlinear in terms of manipulable variables, the behavior at the sampling instants can be made to obey a linear law by varying the number and location of the pulses on each control interval, in addition to the pulse widths. This study discusses various systems for the above exact linearization framework, where the zeros of the derived model can be shifted to the stable area by restricting the region of each control interval in which the pulses are assigned. The zero-stabilization ability is useful in achieving high-speed and high-accuracy positioning/path-following because the inverse of a model that consists of only stable zeros can be used as a feedforward controller. To confirm the effectiveness of the proposed method, a control design for a galvanometer scanner is demonstrated in this study.