LAUSR

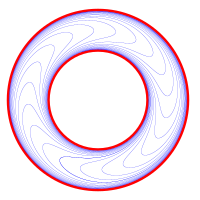
For Reeb graph extraction on surfaces, existing methods always use the isolines of a function defined on the surface to detect the surface components and the neighboring relationships between them. Since such detection is unstable, it is still a challenge for the extracted Reeb graphs to stably and concisely encode the topological information of the surface. In this paper, we address this challenge by using foliation leaves to extract Reeb graphs. In particular, we employ a method for generating measured harmonic foliations by defining loops for foliation initialization and diffusing leaves from loops over the surface. We demonstrate that when the loops are determined, the neighboring relationships between the leaves from different loops are fixed. Thus, we can use loops to represent surface components for robustly detecting the interrelationships between surface components. As a result, we are able to extract stable and concise Reeb graphs. We developed novel measures for loop determination and improved foliation generation, and our method allows the user to manually prescribe loops for generating Reeb graphs with desired structures. Therefore, the potential of Reeb graphs for representing surfaces is enhanced, including conveniently representing the symmetries of the surface and ignoring topological noise. This is verified by our experimental results which indicate that our Reeb graphs are compact and expressive, promoting shape analysis.