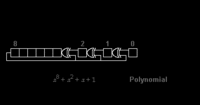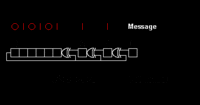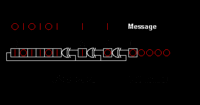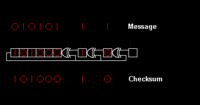
Photo from wikipedia
In this paper, we have shown that a regular Toeplitz matrix-vector product (TMVP) can be transformed into a Toeplitz block TMVP (TBTMVP) using a suitable permutation matrix. Based on the… Click to show full abstract
In this paper, we have shown that a regular Toeplitz matrix-vector product (TMVP) can be transformed into a Toeplitz block TMVP (TBTMVP) using a suitable permutation matrix. Based on the TBTMVP representation, we have proposed a new $(a,b)$ -way TBTMVP decomposition algorithm for implementing a digit-serial multiplication. Moreover, it is shown that, based on iterative block recombination, we can improve the space complexity of the proposed TBTMVP decomposition. From the synthesis results, we have shown that the proposed TBTMVP-based multiplier involves less area, less area-delay product, and higher throughput compared with the existing digit-serial multipliers.
Journal Title: IEEE Transactions on Very Large Scale Integration (VLSI) Systems
Year Published: 2017
Link to full text (if available)
Share on Social Media: Sign Up to like & get
recommendations!