LAUSR

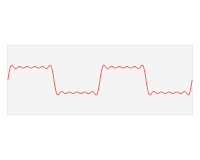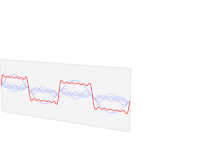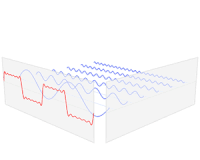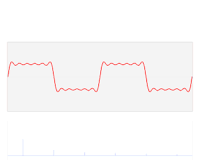
We introduce a generalized sigmoidal transformation on a given interval with a threshold at . Using , we develop a weighted averaging method in order to improve Fourier partial sum approximation for a function having a jump-discontinuity. The method is based on the decomposition of the target function into the left-hand and the right-hand part extensions. The resultant approximate function is composed of the Fourier partial sums of each part extension. The pointwise convergence of the presented method and its availability for resolving Gibbs phenomenon are proved. The efficiency of the method is shown by some numerical examples.