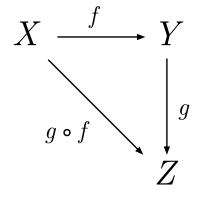
Photo from wikipedia
The purpose of this paper is to build a new bridge between category theory and a 1 generalized probability theory known as noncommutative probability or quantum probability, 2 which was… Click to show full abstract
The purpose of this paper is to build a new bridge between category theory and a 1 generalized probability theory known as noncommutative probability or quantum probability, 2 which was originated as a mathematical framework for quantum theory, in terms of states as linear 3 functional defined on category algebras. We clarify that category algebras can be considered as 4 generalized matrix algebras and that the notions of state on category as linear functional defined 5 on category algebra turns out to be a conceptual generalization of probability measures on sets as 6 discrete categories. Moreover, by establishing a generalization of famous GNS (Gelfand-Naimark7 Segal) construction, we obtain a representation of category algebras of †-categories on certain 8 generalized Hilbert spaces which we call semi-Hilbert modules over rigs. 9
Journal Title: Symmetry
Year Published: 2021
Link to full text (if available)
Share on Social Media: Sign Up to like & get
recommendations!